Eastsheng's Wiki

机器学习基础-3-深度学习

2023-08-01 12:18:28

[toc]

深度学习

  • Tensorflow可以更简洁地实现模型;
  • tensorflow.data模块提供了有关数据处理的工具;
  • tensorflow.keras.layers模块定义了大量神经网络的层;
  • tensorflow.initializers模块定义了各种初始化方法;
  • tensorflow.optimizers模块提供了模型的各种优化算法。

读取数据

  • 将训练数据的特征features和标签labelsl组合
1
2
import tensorflow as tf
dataset = tf.data.Dataset.from_tensor_slices((features, labels))
  • 随机读取小批量
1
2
3
4
5
6
dataset = dataset.shuffle(buffer_size=num_examples) # 随机打乱数据集， buffer_size应>=样本数
dataset = dataset.batch(batch_size) # 分成小数据集，尺寸为batch_size
data_iter = iter(dataset)
for X, y in data_iter: # 读取
    print(X, y)
    break

数据处理

缺失值处理

1
2
dataset.isna().sum() # 查看 dataset为dataframe格式
dataset = dataset.dropna() # 删除

划分数据集

1
2
train_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index)

技巧

自动求梯度

  • 使用tensorflow2.0提供的GradientTape来对$y=2X^TX$自动求梯度：

    1
    2
    3
    4
    5
    6
    7
    x = tf.reshape(tf.Variable(range(4), dtype=tf.float32),(4,1))
    with tf.GradientTape() as t:
        t.watch(x) #对于Variable类型的变量，一般不用加此监控
        y = 2 * tf.matmul(tf.transpose(x), x)

        dy_dx = t.gradient(y, x)
    dy_dx

回归

  • 线性/softmax回归都是一个单层神经网络

  • softmax是一个非线性函数，但softmax回归是一个线性模型（linear model）

    • 线性回归（全连接层）：

    线性回归是一个单层神经网络

    • softmax回归（全连接层）：

    softmax

多层感知机（multilayer perceptron，MLP）

  • 多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络;

  • 每个隐藏层的输出通过激活函数进行变换;

  • 多层感知机的层数和各隐藏层中隐藏单元个数都是超参数;

  • 多层感知机在单层神经网络的基础上引入了一到多个隐藏层（hidden layer）；

  • 隐藏层位于输入层和输出层之间

    • 含有一个隐藏层，该层中有5个隐藏单元；
    • 由于输入层不涉及计算，图中的多层感知机的层数为2；
    • 多层感知机中的隐藏层和输出层都是全连接层；
    • 将隐藏层的输出直接作为输出层的输入；

激活函数

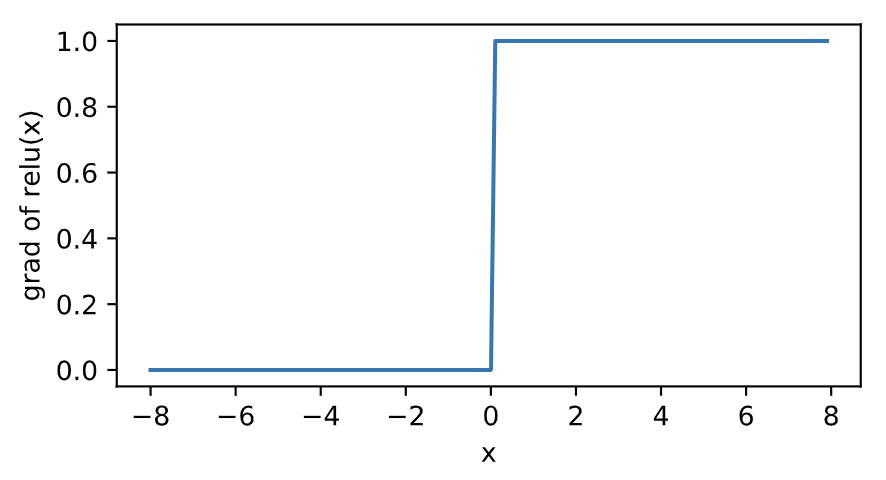
ReLU函数

  • ReLU（rectified linear unit）函数提供了一个很简单的非线性变换：$ReLU(x)=max(x,0)$，其导数：
1
2
3
# tensorflow.nn提供了ReLU函数
import tensorflow as tf
y = tf.nn.relu(x)

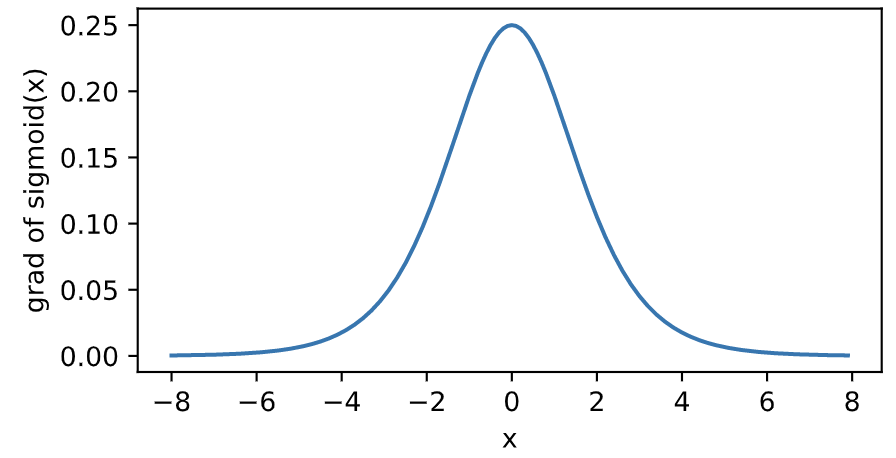
sigmoid函数

  • sigmoid函数可以将元素的值变换到0和1之间：$sigmoid(x)=\frac {1} {1+exp(-x)}$

  • sigmoid函数在早期的神经网络中较为普遍，但它目前逐渐被更简单的ReLU函数取代;

  • sigmoid函数导数：

1
2
# tensorflow.nn提供了sigmoid函数
y = tf.nn.sigmoid(x)

tanh函数

  • tanh（双曲正切）函数可以将元素的值变换到-1和1之间：$tanh(x)=\frac {1-exp(-2x)} {1+exp(-2x)}$;

模型定义与初始化

1
2
3
4
5
6
7
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow import initializers as init
# 使用Keras定义网络，先定义一个模型变量model（Sequential实例），Sequential实例可以看作是一个串联各个层的容器
model = keras.Sequential() 
# 在该容器中依次添加层，这里添加一层，代表线性回归；init随机初始化权重，偏差参数默认为0，标准差为0.01
model.add(layers.Dense(1, kernel_initializer=init.RandomNormal(stddev=0.01)))

损失函数

  • 将衡量误差的函数称为损失函数（loss function）；

  • 在模型训练中，需要衡量预测值与真实值之间的误差；

  • 通常会选取一个非负数作为误差，且数值越小表示误差越小；

  • $l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j$

1
2
import tensorflow as tf
loss = tf.keras.losses.MeanSquaredError()
  • 或者
1
2
from tensorflow import losses
loss = losses.MeanSquaredError()

优化算法

  • 当模型和损失函数形式较为简单时，误差最小化问题的解可以直接用公式表达出来，这类解叫作解析解（analytical solution）；
  • 大多数深度学习模型并没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值，这类解叫作数值解（numerical solution）;
  • 无须自己实现小批量随机梯度下降算法;
  • tensorflow.keras.optimizers 模块提供了很多常用的优化算法比如SGD、Adam和RMSProp等

小批量随机梯度下降

  • 小批量随机梯度下降（mini-batch stochastic gradient descent，MSGD）在深度学习中被广泛使用。
graph TB;
    A[随机选取模型参数初始值]-->B[多次迭代降低损失函数的值];
    B-->C[随机均匀采样一个由固定数目训练数据样本所组成的小批量];
    C-->B;
    C-->D[然后求小批量中数据样本的平均损失有关模型参数的梯度]
    D-->E[用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量]
  • 代码实现：
1
2
from tensorflow.keras import optimizers
trainer = optimizers.SGD(learning_rate=0.03)
  • 批量大小和学习率的值是人为设定的，并不是通过模型训练学出的，因此叫作超参数（hyperparameter）；
  • 通常所说的“调参”指的正是调节超参数，通过反复试错来找到超参数合适的值；
  • 在少数情况下，超参数也可以通过模型训练学出。

误差

  • 训练误差（training error）：模型在训练数据集上表现出的误差；

  • 泛化误差（generalization error）：模型在任意一个测试数据样本上表现出的误差的期望，并常常通过测试数据集上的误差来近似；

    • 使用损失函数（如平方损失函数、交叉熵损失函数）可以计算训练误差和泛化误差；

    • 由于无法从训练误差估计泛化误差，因此一味地降低训练误差并不意味着泛化误差一定会降低；

    • 机器学习模型应关注降低泛化误差。

K折交叉验证

    1. 把原始训练数据集分割成K个不重合的子数据集；
    1. 做K次模型训练和验证；
    1. 每次使用一个子数据集验证模型，并使用其他K−1个子数据集来训练模型；
    1. 在这K次训练和验证中，每次用来验证模型的子数据集都不同；
    1. 最后，对这K次训练误差和验证误差分别求平均。

欠拟合和过拟合

  • 欠拟合（underfitting）：模型无法得到较低的训练误差；

  • 过拟合（overfitting）：模型的训练误差远小于它在测试数据集上的误差；

  • 尽可能同时应对欠拟合和过拟合
  • 两个主要因素：模型复杂度和训练数据集大小

模型复杂度

  • 模型复杂度与误差的关系，以及其对欠拟合和过拟合的影响：

  • 给定训练数据集，如果模型的复杂度过低，很容易出现欠拟合；

  • 如果模型复杂度过高，很容易出现过拟合。

  • 应对欠拟合和过拟合的一个办法是针对数据集选择合适复杂度的模型。

训练数据集大小

  • 一般来说，如果训练数据集中样本数过少，特别是比模型参数数量（按元素计）更少时，过拟合更容易发生。

读取和存储

  • 在实际中，我们有时需要把训练好的模型部署到很多不同的设备
  • 这种情况下，我们可以把内存中训练好的模型参数存储在硬盘上供后续读取使用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# 可以直接使用save函数和load函数分别存储和读取
x = tf.ones(3)
np.save('../data/x.npy', x)
x2 = np.load('../data/x.npy')
x2
# 还可以存储一列tensor并读回内存
y = tf.zeros(3)
np.save('../data/xy.npy',[x,y])
x2, y2 = np.load('../data/xy.npy', allow_pickle=True)
(x2, y2)
# 甚至可以存储并读取一个从字符串映射到tensor的字典
mydict = {'x': x, 'y': y}
np.save('../data/mydict.npy', mydict)
mydict2 = np.load('../data/mydict.npy', allow_pickle=True)
mydict2

# 还可以读写模型的参数
X = tf.random.normal((2,20))
class MLP(tf.keras.Model):
    def __init__(self):
        super().__init__()
        self.flatten = tf.keras.layers.Flatten()    # Flatten层将除第一维（batch_size）以外的维度展平
        self.dense1 = tf.keras.layers.Dense(units=256, activation=tf.nn.relu)
        self.dense2 = tf.keras.layers.Dense(units=10)

    def call(self, inputs):         
        x = self.flatten(inputs)   
        x = self.dense1(x)    
        output = self.dense2(x)     
        return output

net = MLP()
Y = net(X)
Y
# 把该模型的参数存成文件
net.save_weights("../data/4.5saved_model.h5")
# 再实例化一次定义好的多层感知机
# 直接读取保存在文件里的参数
net2 = MLP()
net2(X)
net2.load_weights("../data/4.5saved_model.h5")
Y2 = net2(X)
Y2 == Y

教程

Tags: 机器学习
← Networkx：强大的 Python 网络分析库使用 Ubuntu环境下HTR：水合物分子模拟后处理程序 →